Velocity Obstacles

tags

Motion Planning

Velocity Obstacles are a way to determine collision velocities for agents.

Slides

Starting with Cartesian

Imagine starting with a Cartesian space where there are two agents, \(A\) and \(B\).

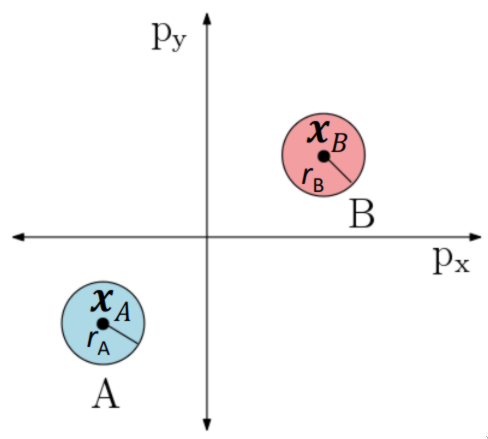
Now if you translate this space so that \(A\) is centered at the origin and \(B\) is at position \(x_{b}-x_{a}\).

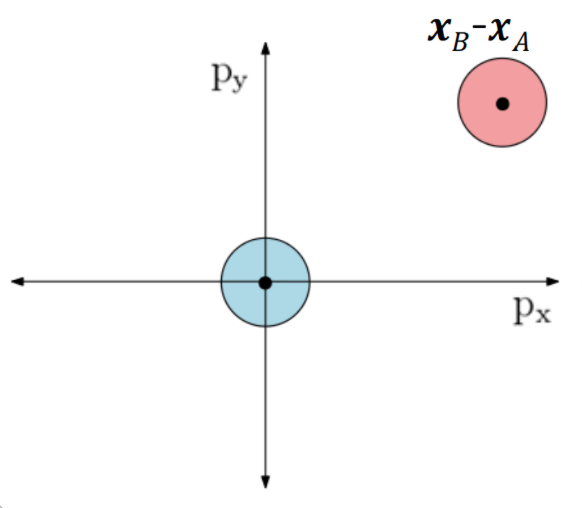
Now if you deflate \(A\) so that it is a single point, then inflate \(B\) so it has a has a radius of \(r_{a}+r_{b}\) (because \(A\) is a point and the radius has to be increased).

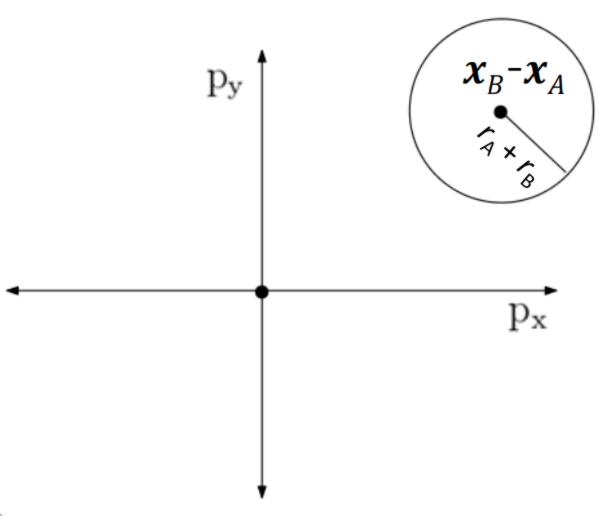
By doing this you calculate the Minkowski sum. Remember the Minkowsi sum \(X \oplus Y = \{ x + y | x \in X, y \in Y \}\). So if \(X\) is the position of \(A\) (\(\{[0, 0]\}\)), and \(Y\) is the position of \(B\) (\(\{[1, 1]\}\)). Then \(X \oplus Y = \{[1, 1]\}\).

To Velocity Space

If we take that same 2d plane but change the \(X\) and \(Y\) axis and change them to velocities (by dividing everything by one second).

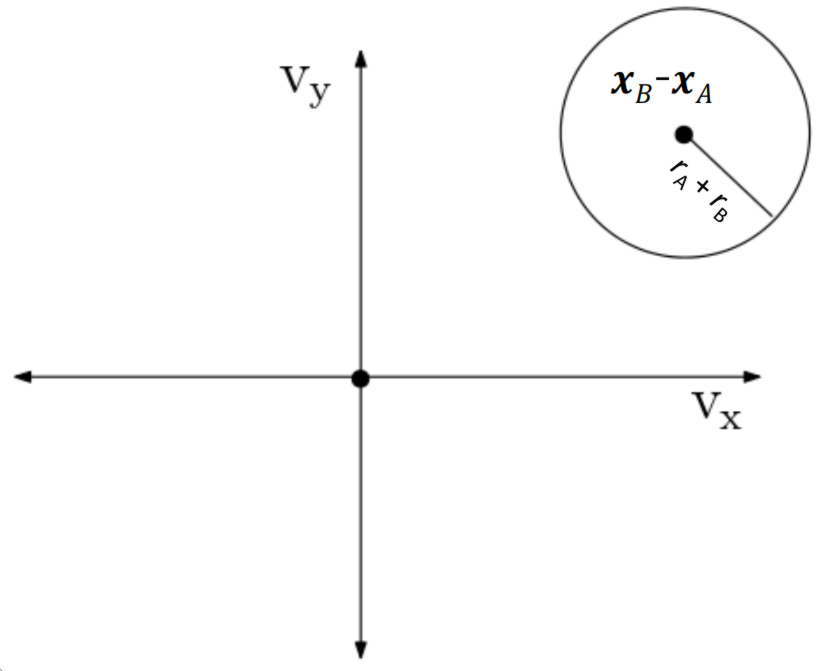
Now every point in this space denotes a velocity. The question now is what is the set of velocities that will lead to a collision. This set is the \(VO_{A|B}\), or the velocity obstacle of \(A\) induced by \(B\).

To find if a some velocity \(\vec{V}_{1}\) is a collision velocity then have it define a ray starting at the origin and passing through \(\vec{V}_1\). If this ray intersects the disk then it is a collision velocity. Writing the point of intersection in the form of \(\tau \vec{V}_{1}\) where \(\tau\) is some constant gives you the time til collision.

Revising definition

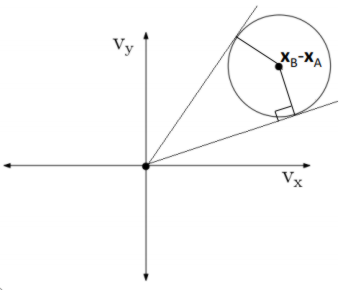
The velocity obstacle can be geometrically defined as the following:

\begin{equation} \label{eq:1} VO_{{A|B}} = \{ \vec{v} | \exists \tau \ge 0 : \tau \vec{v} \cap \in D(x_{B} -_{} x_{A}, r_{A} + r_{B}) \ne \emptyset\} \end{equation}

In English this means that the velocity obstacle of A induced by B is the set of all velocities such that there exists a constant \(\tau \ge 0\) such that \(\tau \vec{v}\) is within the disk centered at \(x_{B}-x_{A}\) with radius \(r_{A}+r_{B}\).

This definition gives a cone with its apex at the origin and its sides running tangent to the disk.

Time Horizon Velocity Obstacle

A time horizon Velocity Obstacle is a \(VO\) that describes velocities that will lead to a collision between time \(0\) and some time \(\tau_{{H}}\). This is useful if you don’t care about collisions that will happen far in the future.

Given two agents, \(A\) and \(B\), the velocity obstacle \(VO^{\tau_{H}}_{A|B}\) (read: the velocity obstacle of \(A\) induced by \(B\) for time horizon \(\tau_{H}\)) is the set of all velocities that \(A\) can take that will lead to a collision between \(A\) and \(B\) at some moment within the next \(\tau_{H}\) seconds. The geometric definition is as follows:

\begin{equation} \label{eq:2} VO^{\tau_{H}}_{A|B} = \{ v | \exists \tau \in [0, \tau_{H}]: \tau V \cap \in D(x_{B} - X_{A}, r_{A} + r_{B}) \ne \emptyset \} \end{equation}

In english this means that the velocity obstacle, \(VO\), for a time horizon \(\tau_{H}\) induced on \(A\) by \(B\) is equal to all velocities such that a \(\tau\) exists between \(0\) and \(\tau_{H}\) (inclusive) such that \(\tau V\) unioned with the disk centered at \(X_{B} - X_{A}\) with radius \(r_{A} + r_{B}\) is not empty.

Geometrically, this \(VO\) is still a cone (assuming circular agents). But this cone is truncated by a disk of radius \(\frac{r_{A} + r_{B}}{\tau_{H}}\) and centered at \(\frac{x_{A} - x_{B}}{\tau_{H}}\) compared to the \(VO\) discussed above.

GOT TO 24:40 ish